Measures of Dispersion

Introduction

• Measures of central tendency (mean, median, mode) describe where data points are centered but do not indicate how spread out the data is around the center.¹
• To capture variation or spread, measures of dispersion are used.¹
• Commonly used measures of dispersion include:
  • Range – the difference between the largest and smallest values^1,2
  • IQR – the spread of the middle 50% of values^1,2
  • SD – average distance of values from the mean^2,3
  • Variance (s²) – the squared average deviation from the mean⁴
  • CV – standard deviation relative to the mean⁵
• These measures help describe the consistency or variability within a dataset.¹
• Low variability indicates that values are closely grouped, reflecting higher precision.¹
• High variability indicates that values are spread out, reflecting lower precision and greater dispersion.¹

Range and IQR

Range

• The simplest measure of variability is the range, which is the difference between the largest and smallest points in a dataset.^1,2
• Advantages:
  • Easy and quick to calculate.²
• Disadvantages:
  • It is based solely on two values and disregards the rest of the data.²
  • It is highly sensitive to outliers, which can skew findings.²

Example:

Suppose a study records systolic blood pressures during anesthetic induction for 10 patients, with the following findings: 90, 93, 97, 99, 101, 102, 104, 106, 108, 145 mmHg.

• The range of this data set is 145 – 90 = 55 mmHg.
• However, 145 mmHg may represent an outlier.
  • This makes the range a less accurate reflection of the overall dataset, where most values fall between 90 and 108 mmHg.
• In this situation, a more robust measure such as the IQR may offer a clearer representation of the data’s variability.

IQR

• An alternative to the range is the IQR, which provides a more robust measure of variability.^1,2,4
• Quartiles divide a dataset into four equal parts.⁴
• Other subdivisions include:⁴
  • Tertiles (three groups)
  • Quintiles (five groups)
  • Deciles (ten groups)
• The IQR represents the range between the first quartile (Q1) and the third quartile (Q3), capturing the middle 50% of the data.⁴
• IQR is resistant to outliers, making it useful when the data are skewed or not symmetrically distributed, which contrasts with range.²

Example:

A study records postoperative pain scores for 10 patients following surgery with the following scores: 2, 3, 4, 4, 5, 5, 6, 7, 8, 10.

IQR Calculation:

• Q1 (25th percentile): Average of the 3rd and 4th values = (4 + 4) / 2 = 4
• Q3 (75th percentile): Average of the 8th and 9th values = (7 + 8) / 2 = 7.5
• IQR = Q3 – Q1 = 7.5 – 4 = 3.5

Interpretation:

• Although the range is 8 (10-2), the IQR of 3.5 shows that the middle 50% of patients had pain scores between 4 and 7.5.
• Reporting the IQR gives a more accurate picture of patient experiences than the full range, which overemphasizes extreme values.

Variance, SD, and CV

Variance

• The sample variance (denoted as s²) is the average of the squared differences from the mean.^1,3,4 It is calculated using the following formula:¹

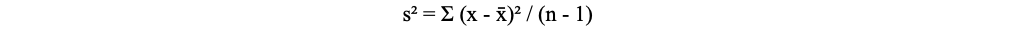
• • x = each individual value
  • x̄ = sample mean
  • n = number of observations
• It provides a numerical estimate of data spread or dispersion.¹
• It is always non-negative, as variance can never be less than zero.³
  • Variance equals zero only when all values in the dataset are identical.³
• A smaller variance indicates that the values tend to congregate around the mean.³
• A larger variance suggests that at least some values are far from the mean.³
• Variance is the penultimate step in calculating standard deviation.¹

Clinical Significance of Variance

• In clinical practice, variance helps determine how a patient’s measurement is compared to a reference population.³
• Reference ranges in laboratory tests (e.g., serum sodium or hematocrit) are typically calculated using the mean ± a multiple of the variance, helping clinicians interpret individual values.³
• In anesthesiology, understanding variance helps guide the selection of drugs.
  • Medications with longer half-lives and slower metabolism often exhibit lower variability in blood levels, resulting in more consistent effects and a reduced risk of over- or underdosing.³

SD

• SD is the most widely used measure of dispersion in quantitative data.²
• It reflects how spread out the individual observations are around the mean.^2,3
• Conceptually, SD answers “how far each value is from the mean?”⁶
• SD is calculated using the following formula²

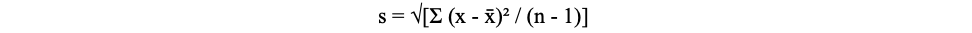
• • x = each individual value
  • x̄ = sample mean
  • n = number of observations
• A small SD suggests that values congregate around the mean.¹
• A large SD indicates that the data are widely spread out from the mean.⁶

SD and the Normal Distribution

• In a normally distributed dataset:^2,6
  • ~68.3% of values fall within the mean ± 1 SD
  • ~95.5% fall within the mean ± 2 SD
  • ~99.7% fall within the mean ± 3 SD
• This property allows SD to be used for probability estimates and standardized comparisons.⁶

Example:

A study measures the induction dose of propofol administered to 25 adult patients undergoing general anesthesia. The data shows the following:

• Mean dose = 2.0 mg/kg
• SD = 0.2 mg/kg

Interpretation:

• The mean indicates that, on average, patients received 2.0 mg/kg of propofol.
• The SD of 0.2 mg/kg suggests that most doses were relatively close to the mean, falling between 1.8 and 2.2 mg/kg.
• Assuming normal distribution, it can be expected that the following is true:
  • ~68% of patients received between 1.8 and 2.2 mg/kg
  • ~95% received between 1.6 and 2.4 mg/kg

CV

• The coefficient of variation (CV) is a measure of relative dispersion, expressing the standard deviation as a percentage of the mean.⁵
• It is calculated using the following formula:⁵

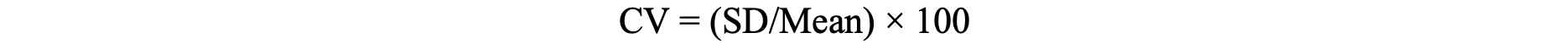
• CV allows for comparisons to be made between datasets that differ in scale or units.⁵
  • The CV is unitless, making it especially useful when comparing variability across measurements that have different magnitudes (e.g., heart rate vs. blood pressure).⁵
• The CV is appropriate only when data are measured on a ratio scale which have a true zero point.⁵
• Standard methods for inference with CV often rely on the assumption that the data are normally distributed.⁵