Copy link
Venous Access and Poiseuille Law
Last updated: 02/16/2023
Key Points
- In the trauma setting, obtaining timely vascular access should be prioritized.
- Poiseuille’s law describes the laminar flow rate of fluids through intravenous (IV) catheters and helps guide our choice of vascular access.
- Rapid infusion systems are excellent tools for quickly and safely delivering large volumes of crystalloid and blood products.
Introduction
- In the trauma setting, obtaining vascular access in a timely fashion is critical for maintaining adequate end-organ perfusion, which is essential for survival.
- The traditional sequence of trauma care, ABC (Airway, Breathing, Circulation), which prioritizes airway management before circulation has limited scientific evidence and has been questioned.1 In hypovolemic patients, the vasodilatory response following rapid sequence induction, and decreased venous return following the initiation of positive pressure ventilation further reduces cardiac output and end-organ perfusion.1 A multicenter retrospective trial that compared prioritizing circulation before airway management to the traditional ABC sequence showed equivalent mortality outcomes.1
Venous Access
- Vascular cannulation is the cornerstone of resuscitation in the trauma setting. During the primary assessment of an adult trauma patient, at least two large-bore IVs (16-gauge or larger) should be placed. IV access should be obtained above the diaphragm in patients with major abdominal or pelvic trauma secondary to risk of injury to the inferior vena cava.2
- If peripheral IV placement attempts are unsuccessful, central venous access should be obtained. Potential sites for central venous access are the internal jugular, subclavian, and femoral veins.2
- The subclavian vein is commonly chosen for central venous access because it’s easily accessible and is seldom directly traumatized. However, it carries the risk of pneumothorax.
- The femoral vein is also easily accessible but is associated with a higher risk of formation of deep vein thrombosis.
- The internal jugular vein is rarely accessible in the acute trauma setting, secondary to the presence of the cervical collar.
- While the trauma setting is a hectic environment, sterile techniques should always be used when performing any invasive procedure. Always remember to prep appropriately and use sterile equipment.
- The use of ultrasonography is recommended while obtaining central venous access.
Poiseuille’s Law
- The laminar flow rate of fluids through an IV catheter is described by Poiseuille’s law, which states that the flow rate depends on several factors, including the pressure gradient across the tubing, viscosity of the fluid, radius, and length of the tubing.

Figure 1. Poiseuille’s equation
Radius
- Increasing the radius of the tubing has the greatest effect on the flow rate. Doubling the radius of the IV catheter increases the flow rate by 16-fold (Table 1). In general, large-bore peripheral IVs will deliver fluids more rapidly than central venous catheters due to the shorter catheter length and larger radius.
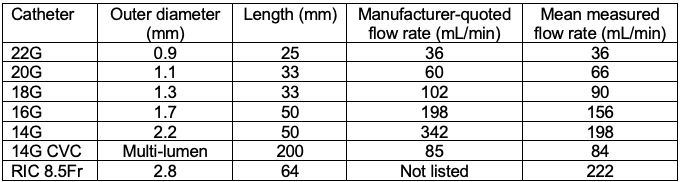
Table 1. Mean flow rates through venous catheters. CVC = central venous catheter, RIC = rapid-infuser catheter. Adapted from Khoyratty SI, et al. Flow rates through intravenous access devices: an in vitro study. J Clin Anesth. 2016; 31: 101-5.3
Tubing Length
- Flow rates are inversely proportional to the length of the catheter.
Fluid Viscosity
- Flow rates are inversely proportional to the viscosity of the fluid. Poiseuille’s equation governs laminar flow rates in noncompressible Newtonian fluids (e.g., crystalloids) with constant viscosity. The viscosity of common intravenous fluids are:
- lactated Ringer’s solution- 1.0 centiPoise;
- hetastarch- 4.0 centiPoise;
- 5% albumin- 40.0 centiPoise.
- In non-Newtonian fluids with variable viscosity (e.g., blood products), other factors such as hematocrit and blood shear rates, velocity gradient of blood as it moves from the vessel wall (low velocity) to vessel lumen (high velocity) also affect the flow rates.
• Rapid infusions systems can also alter the fluid’s viscosity by rapidly warming it to physiologic temperatures.
Pressure Gradient
- Increasing the pressure gradient by using gravity, pressure bags, or infusion devices increases flow rates.
Rapid Infusion Systems
- Rapid infusion systems are often used in the trauma setting to rapidly replace lost volume by increasing flow due to their ability to increase pressure and decrease the viscosity of the fluid given.
- There are several common features of rapid infusion systems.2
- They contain a roller pump that allows the rapid administration of fluids up to 1500 mL/min.
- A wide range of fluids, including crystalloids, colloids, packed red blood cells (PRBC), fresh frozen plasma (FFP), etc., can be administered. Platelets and cryoprecipitate should NOT be administered via rapid infusion systems.
- Fluids are heated to controlled temperatures (38-40℃) before infusion.
- A reservoir allows the mixing of fluid and blood products in preparation for rapid blood loss.
- These devices typically limit infusion pressures to approximately 300 mmHg.
- The presence of fail-safe systems (air and pressure sensors) prevents the infusion of air.
- They also allow accurate recording of the fluid volume administered.
- Two commonly used rapid infusion systems are:
- Belmont® Rapid Infuser RI-2 (Belmont Medical Technologies, Billerica, MA) Link
- Uses electromagnetic induction heating (Figure 2)
- Belmont® Rapid Infuser RI-2 (Belmont Medical Technologies, Billerica, MA) Link

Figure 2. Belmont® Rapid Infuser RI-2. Reproduced with permission from Belmont Medical Technologies, Billerica, MA.
- Level1® H-1200 Fast Flow Fluid Warmer (ICU Medical, Minneapolis, MN) Link
- Uses an aluminum heat exchanger and countercurrent water bath to warm up IV fluids
- Uses pressurized air to compress the IV bags (Figure 3)

Figure 3. Level1® H-1200 Fast Flow Fluid Warmer. Reproduced with permission from ICU Medical, Minneapolis, MN.
- Despite anecdotal case reports of overheating and shutdown of Belmont® Rapid Infusers, an experimental study did not observe any significant overheating under extreme operating conditions.4 The researchers noted that adding large amounts of CaCl2 to the reservoir resulted in the clotting of blood products, thereby reinforcing the recommendation that calcium-containing products should not be administered in the same line as citrated blood products.
- When using rapid infusion systems, patient IV extensions should be avoided, if possible. A study evaluating the maximum flow rates of a mixture of PRBC and FFP through IV catheters of different sizes and a Belmont® rapid infuser system reported that adding patient line extensions reduced the conductance of wider bore IV catheters by approximately 20%.5
References
- Ferrada P, Callcut RA, Skarupa DJ, et al. Circulation first - the time has come to question the sequencing of care in the ABCs of trauma; an American Association for the Surgery of Trauma multicenter trial. World J Emerg Surg. 2018; 13:8. PubMed
- Galvagno SM, Steurer MP, Grisson TE. Anesthesia for Trauma. In: Gropper MA (ed). Miller’s Anesthesia. 9th edition. Philadelphia, PA. Elsevier. 2019. 2115-55.
- Khoyratty SI, Gajendragadkar PR, Polisetty K, et al. Flow rates through intravenous access devices: an in vitro study. J Clin Anesth. 2016; 31: 101-5. PubMed
- Boyer B, Hocking KM, Booth GS, et al. An evaluation of inducted failure modes in the Belmont Rapid Infuser. Anesth Analg. 2016; 122(4): 1062-9. PubMed
- Milne A, Teng JJ, Vargas A, Markley JC, Collins A. Performance assessment of intravenous catheters for massive transfusion: A pragmatic in vitro study. Transfusion. 2021;61(6):1721-1728. PubMed
Copyright Information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.